1. ¿Cuántas ternas ordenadas de números enteros y positivos (a, b, c) distintos de la unidad hay tales que

2. Dibuja una semicircunferencia con centro en O y diámetro AB y, en su interior, otra, con diámetro OA. Traza por un punto C de OA una recta perpendicular a dicho segmento OA, que cortará a la semicircunferencia pequeña en D y a la grande en E y, finalmente, la recta AD que cortará al semicírculo grande en F.
   Demuestra que la circunferencia circunscrita al triángulo DEF es tangente a la cuerda AE en E

3. ¿Cuál es el número máximo de vértices que podemos elegir de un polígono regular de 21 lados para que, al trazar los
segmentos que los unen entre sí, no haya dos con la misma longitud?
 
 

4. Determina los dos valores de x más próximos (por defecto y por exceso) a 2003º que cumplen la siguiente ecuación
trigonométrica:

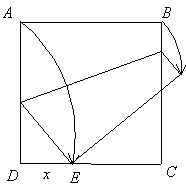
5. Un cuadrado de papel ABCD se dobla de modo que el vértice A toque en un punto arbitrario E del lado CD. Así, se obtienen tres triángulos rectos formados por una sola capa de papel.
   Determinar la longitud de sus lados en función de x = DE para demostrar que el perímetro del triángulo mayor es la suma de los perímetros de los otros dos, y vale la mitad que el perímetro del cuadrado. (Teorema de Haga) .

6. Dado el polinomio p(x) = x³ + Bx² + Cx + D, prueba que si el cuadrado de una de sus raíces es igual al producto de las otras dos, entonces B³D = C³.

1. Se dispone de pequeñas piezas de madera de tamaño 4 x 5 x 10. Decide si es posible o no apilarlas, sin dejar huecos y
apoyándolas siempre sobre cualquiera de sus caras, para formar un ortoedro de dimensiones 2²⁰⁰³ x 3²⁰⁰³ x 5^2003.
 

2. Dado un triángulo de vértices A, B y C,y con lados de longitud a = BC, b = AC y c = AB, llamemos D al punto de
intersección del lado AB con la bisectriz del ángulo C. Demuestra que:

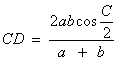
3.  ¿Existirán 16 números naturales distintos y menores de 100 tales que al colocarlos en las casillas de un tablero 4 x 4 el
producto de los situados en cada fila sea el mismo y, a su vez, coincida con el de los colocados en cada columna y en las dos
diagonales principales.?
   Si la respuesta es afirmativa, indica cuáles son.
   Si la respuesta es negativa, justifícalo.

4.  Prueba que si los números loga x, logb x y logc x  (con x distinto de 1) están en progresión aritmética, entonces

6. Por turno, en orden alfabético, tres amigos lanzan un dado. Quien saque un 6 en primer lugar gana lo apostado.
Por cada euro que apueste Carlos, ¿qué cantidad han de poner Ana y Blas para equilibrar el juego y lograr que sea equitativo, es decir, para que las expectativas de ganancia sean las mismas para los tres colegas y no se vean afectadas por el orden de actuación al lanzar el dado?